1. DEFINIÇÃO
Sejam a e b números reais positivos diferentes de zero e b diferente de 1. Chama-se logaritmo de a na base b o expoente x tal que bx = a:
logb a = x bx = az
Na sentença logb a = x temos:
a) a é o logaritmando;
b) b é a base do logaritmo;
c) x é o logaritmo de a na base b.
Exemplos:
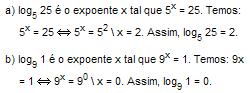
Observação 1: Quando a base não vier expressa, fica subentendido que esta vale 10.
Exemplos:
a) log 3 = log 10 3
b) log 20 = log10 20
Condições de existência
a) A base tem de ser um número real positivo e diferente de 1.
b) O logaritmando tem de ser um número real positivo.
2. PROPRIEDADES DOS LOGARITMOS
a) O logaritmo de um número, na base de valor igual a ele mesmo, é sempre igual a 1.
log b b = 1.
Exemplo:
log8 8 = 1.
b) O logaritmo de 1 em qualquer base é sempre igual a 0.
log b 1 = 0
Exemplo:
log9 1 = 0
c) Logaritmo de uma potência
log b ay = y. logb a
Exemplo:
Log2 34 = 4. log2 3
d) O logaritmo de um número b, na base b, elevado a um expoente x é sempre igual a x.
log b bx = x
Exemplo:
Log 3 37 = 7
e) Um número b, elevado ao logaritmo de a na base b, é sempre igual a a.
b logb a = a
Exemplo:
7 log7 13 = 13
f) Logaritmo do produto:
log c (m . n) = logc m + logc n, sendo m > 0, n > 0 e b 1.
Exemplo:
log2 (4 . 3) = log2 4 + log2 3
g) Logaritmo do quociente:
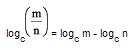

Exemplos:
a) log 3 = log 10 3
b) log 20 = log10 20
Condições de existência
a) A base tem de ser um número real positivo e diferente de 1.
b) O logaritmando tem de ser um número real positivo.
2. PROPRIEDADES DOS LOGARITMOS
a) O logaritmo de um número, na base de valor igual a ele mesmo, é sempre igual a 1.
log b b = 1.
Exemplo:
log8 8 = 1.
b) O logaritmo de 1 em qualquer base é sempre igual a 0.
log b 1 = 0
Exemplo:
log9 1 = 0
c) Logaritmo de uma potência
log b ay = y. logb a
Exemplo:
Log2 34 = 4. log2 3
d) O logaritmo de um número b, na base b, elevado a um expoente x é sempre igual a x.
log b bx = x
Exemplo:
Log 3 37 = 7
e) Um número b, elevado ao logaritmo de a na base b, é sempre igual a a.
b logb a = a
Exemplo:
7 log7 13 = 13
f) Logaritmo do produto:
log c (m . n) = logc m + logc n, sendo m > 0, n > 0 e b 1.
Exemplo:
log2 (4 . 3) = log2 4 + log2 3
g) Logaritmo do quociente:
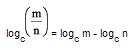








0 comentários:
Postar um comentário