Resolvendo o sistema 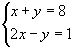 , encontramos uma única solução: o par ordenado (3,5). Assim, dizemos que o sistema é possível (tem solução) e determinado (solução única).
, encontramos uma única solução: o par ordenado (3,5). Assim, dizemos que o sistema é possível (tem solução) e determinado (solução única).
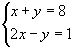 , encontramos uma única solução: o par ordenado (3,5). Assim, dizemos que o sistema é possível (tem solução) e determinado (solução única).
, encontramos uma única solução: o par ordenado (3,5). Assim, dizemos que o sistema é possível (tem solução) e determinado (solução única).
No caso do sistema 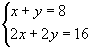 , verificamos que os pares ordenados (0,8), (1,7),(2,6),(3,5),(4,4),(5,3),...são algumas de suas infinitas soluções. Por isso, dizemos que o sistema é possível (tem solução) e indeterminado (infinitas soluções).
, verificamos que os pares ordenados (0,8), (1,7),(2,6),(3,5),(4,4),(5,3),...são algumas de suas infinitas soluções. Por isso, dizemos que o sistema é possível (tem solução) e indeterminado (infinitas soluções).
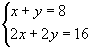 , verificamos que os pares ordenados (0,8), (1,7),(2,6),(3,5),(4,4),(5,3),...são algumas de suas infinitas soluções. Por isso, dizemos que o sistema é possível (tem solução) e indeterminado (infinitas soluções).
, verificamos que os pares ordenados (0,8), (1,7),(2,6),(3,5),(4,4),(5,3),...são algumas de suas infinitas soluções. Por isso, dizemos que o sistema é possível (tem solução) e indeterminado (infinitas soluções).
Para 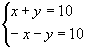 , verificamos que nenhum par ordenado satisfaz simultaneamente as equações. Portanto, o sistema é impossível (não tem solução).
, verificamos que nenhum par ordenado satisfaz simultaneamente as equações. Portanto, o sistema é impossível (não tem solução).
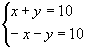 , verificamos que nenhum par ordenado satisfaz simultaneamente as equações. Portanto, o sistema é impossível (não tem solução).
, verificamos que nenhum par ordenado satisfaz simultaneamente as equações. Portanto, o sistema é impossível (não tem solução).Resumindo, um sistema linear pode ser:
a) possível e determinado (solução única);
b) possível e indeterminado (infinitas soluções);
c) impossível (não tem solução).
b) possível e indeterminado (infinitas soluções);
c) impossível (não tem solução).
Discussão de um sistema linear
a) possível e determinado, se D=det A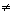 0; caso em que a solução é única.
0; caso em que a solução é única.
Exemplo:
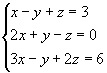
m=n=3
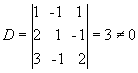
Então, o sistema é possível e determinado, tendo solução única.
b) possível e indeterminado, se D= Dx1 = Dx2 = Dx3 = ... = Dxn= 0, para n=2. Se n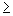 3, essa condição só será válida se não houver equações com coeficientes das incógnitas respectivamente proporcionais e termos independentes não-proporcionais.
3, essa condição só será válida se não houver equações com coeficientes das incógnitas respectivamente proporcionais e termos independentes não-proporcionais.
Um sistema possível e indeterminado apresenta infinitas soluções.
Exemplo:
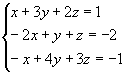
D=0, Dx =0, Dy=0 e Dz=0
Assim, o sistema é possível e indeterminado, tendo infinitas soluções.
c) impossível, se D=0 e 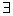 Dxi
Dxi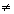 0, 1
0, 1 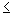 i
i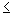 n; caso em que o sistema não tem solução.
n; caso em que o sistema não tem solução.
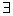 Dxi
Dxi
Exemplo:
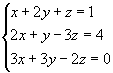
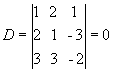
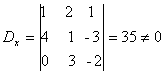
Como D=0 e Dx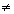 0, o sistema é impossível e não apresenta solução.
0, o sistema é impossível e não apresenta solução.







0 comentários:
Postar um comentário